時間複雜度

為什麼要學 Big O

學習演算法和資料結構就是為了寫出高效率的程式碼，不只在時間上需要快速，在空間上的消耗更要節省，而 Big O 就是用來衡量演算法效率的單位。因此，在學習各種資料結構與演算法帶來的好處之前，要先懂得如何透過 Big O 辨別程式碼的效率。

時間複雜度也稱為漸進執行時間 (asymptotic runtime) ，用來表達隨著資料規模的變大，執行時間如何放大。在計算複雜度時，不用執著於最精準的執行時間，細節需要考慮到組合語言層次與編譯器等問題，這樣做太複雜，我們只需要接受 O(N) 一定比 O(N^2) 好。

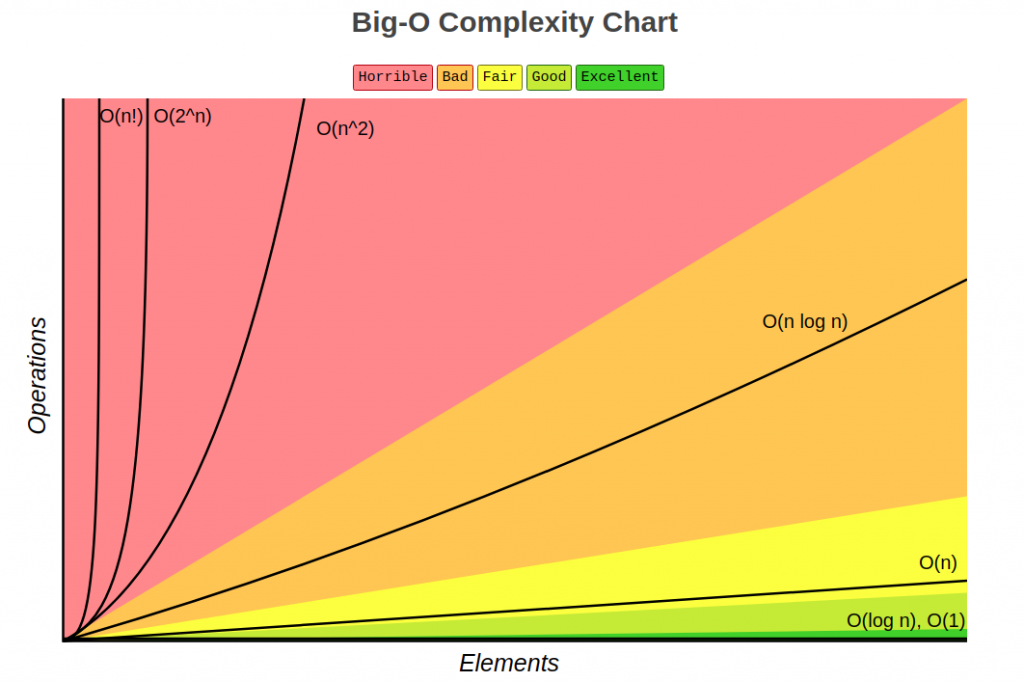
資料來源：https://www.bigocheatsheet.com/

只關心最壞的情況（業界對時間複雜度的使用方式：對執行時間以最緊的標準來描述。）
移除常數
Big O 只描述增加的速率，因此可以降低執行時間的常數，描述為 O(2N^2) 的演算法實際上表示為 O(N^2) 即可。
降低非優勢條件
像 O(N^2 + N) ，第二個 N 完全不重要，在移除常數說過，O(N^2 + N^2) 可視為 O(N^2) ，竟然後面 N^2 都不在乎了，這邊的 N 也可以完全捨去。
- O (N + logN) 變成 O (N)
- O (3* 2^N + 1000 * N^100) 變成 O (2^N)
多步驟演算法：加與乘
假設演算法有兩個步驟，什麼時候相加或相乘執行時間呢？

for (int i : A)
    print i;
for (int j : B)
    print j;

for (int i : A)
    for (int j : B)
        print i + j;

上方程式是先執行 A 再執行 B ，因此時間複雜度為 O (A+B) 。
下方程式每次執行一次 A ，會再執行一次 B ，因此時間複雜度為 O (A * B)

可以歸納為

int f(int n) {
    if (n<=1) {
        return 1;
    }
    return f(n-1) + f(n-1);

許多人看到有兩個 f(n) 的呼叫，就認為是 O(n^2) ，這不是對的。

實際走一遍程式碼，你會發現整個執行過程如同二元樹，每次呼叫遞迴函式會再呼叫兩個遞迴函式，就如同一個節點會有兩個子節點。因此，每一層都比上一層多一倍呼叫。

嘗試記住這個表！遇到遞迴函式時，執行時間通常看起來像 O (分支 ^ 深度) ，分支為每個遞迴呼叫再次呼叫的數量，因此，這個遞迴函式時間複雜度為 O (2^n) 。

假設有個演算法將字串陣列的每個字串排序後再排序整個陣列，執行時間是什麼？

很多人會這麼看：字串排序是 O(N log N) ，每個字串都要執行，因此是 O(N * N log N) 。我們還需要排序陣列，因此還要一個 O ( N log N) 。所有全部執行時間為 O ( N^2 log N + N Log N) ，也就是 O ( N^2 log N ) 。

以上說法完全錯誤！

第一個錯誤，不能以 N 來表達兩個不一樣的長度，一個是字串的長度，一個是字串陣列內的字串數量，面試時，記得要清楚定義你的 N 。

讓我們清楚定義長度，並給予合理的名稱。

接下來可以這樣計算：

對單一字串排序所需時間為 O ( s log s ) ，總共有 a 個字串，因此所有的字串需要 O (a * s log s) 。
對所有字串排序，因為有 a 個字串，排序所有字串要花時間為 O ( a log a ) 時間。但是還要考慮到字串比較時，字串內的每個字元可能還需要進一步比較，又需要 O (s) 的時間，因此總共需要花 O (s * a log a) 時間。

整個過程需要上面兩個時間複雜度相加 O (a * s * (log a + log s) ) 。

空間複雜度也稱為 asymptotic space complexity ，表達隨著資料規模增大，程式所需空間如何增大。

需要計算消耗空間的因素有：

需特別注意，遞迴呼叫所需的堆疊 ( stack ) 空間也需要計算。下面程式需要 O(n) 的時間與 O(n) 的空間。

int sum (int n) {
    if (n <= 0) {
        return 0;
    }
    return n * sum (n-1);
}