Leetcode 邁向千題的關卡，想要把所有題目刷過一遍，對於一位上班族來說就跟寫出來的程式沒有 bug 一樣困難，因此想要將刷題常用的觀念技巧與其對應題目整理出來，一方面可以整理自己思緒，也可以做為未來複習用。
這系列文章會一直持續下去，算是作為工程師職涯的隨身裝備。

何時使用 BFS

1. 尋找兩點間 最短距離
2. Tree 的 level order traversal

BFS 比 DFS 更適合用來解決尋找最短距離的問題，其代價則是需耗費較大的空間複雜度。

BFS 操作框架

典型的 BFS 需要以下三種資料結構：

1. 透過 queue 的 FIFO 特性來紀錄走訪過且待處理的 vertex (頂點) 。
2. 用 visited 陣列來記錄各 vertex 是否被走訪過，避免 vertex 被重複訪問。
   • 如果圖是 binary tree ，就不會有重複造訪的情況，就不需要 visited 陣列 。
   • 如果 vertex 不是由固定範圍的 integer 所構成 ，可以用 hash table 的資料結構來紀錄頂點是否走訪過 （以 C++ 來說，可以用 unordered_set ）
3. 用 prev 來紀錄搜尋路徑。 prev[s] = t ，代表由 t 走到 s ，也就是說 prev[s] 表示頂點 s 是由哪個頂點走過來的 。

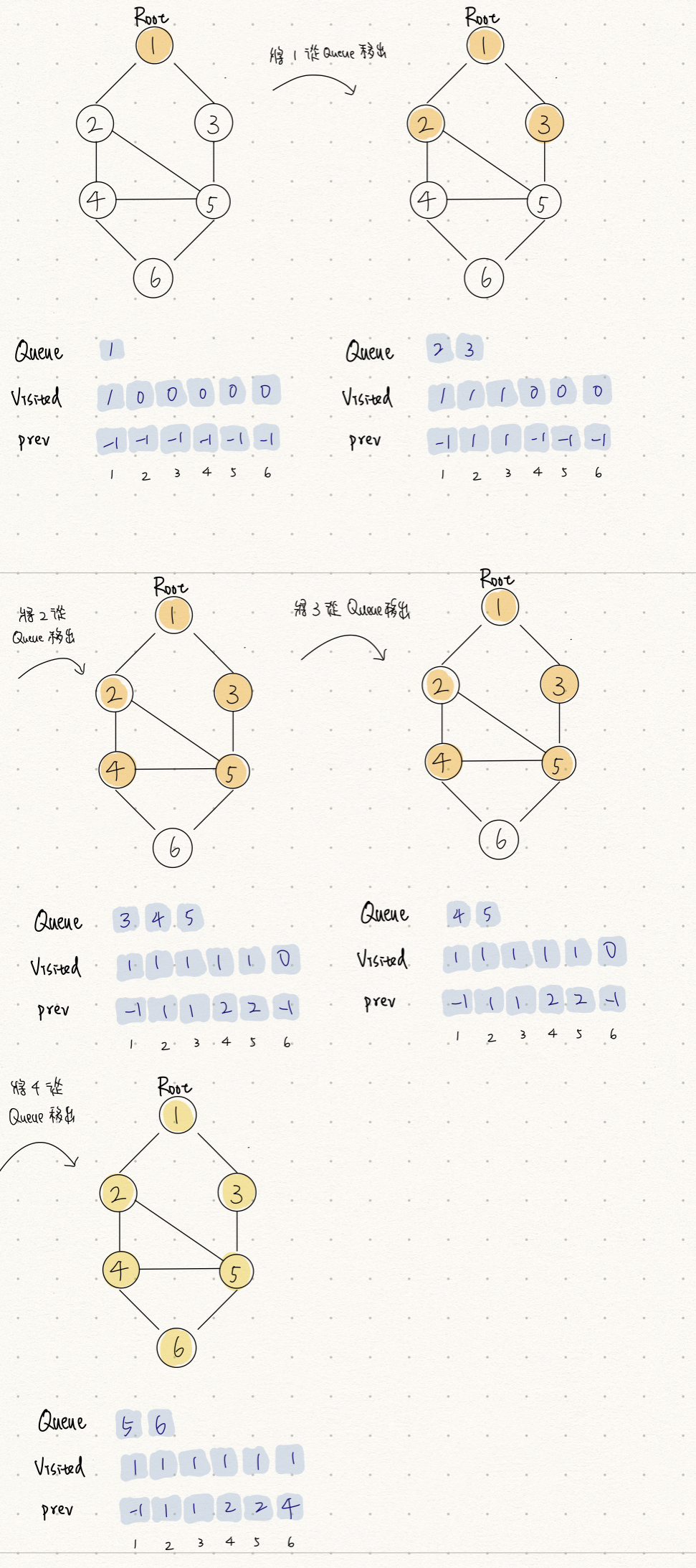
BFS 操作順序如下，可以搭配下面的示意圖與程式碼來理解：

1. 把起點放到 queue 裡，並將其在 visited 陣列中對應值寫成 1 表示拜訪過 。
2. 從 queue 的前端拿出最早放入的 vertex (queue 的 FIFO 特性 ）。
3. 檢查拿出的 vertex 的所有鄰近 vertices 中，將尚未走訪過的放進 queue 中，並執行以下動作：
   1. 將其在 visited 陣列中對應值寫成 1
   2. 將其在 prev 陣列中對應值寫成拿出的 vertex
4. 移除 queue 前端的 vertex 。
5. 不斷重複步驟 2~4 直到 queue 為空。

BFS 的走訪順序可以由以下兩種方式找出:

1. 每次從 queue 拿出元素時
2. 由 prev 陣列構建出 BFS 的走訪順序。

int BFS (int start, int target)
{
    queue<int> qu;
    int shortest_step = 0;
    int visited[size] = {0};
    int prev[size] = {-1};

    qu.push (start);
    while (!qu.empty ())
    {
        int round = q.size ();
        for (int i=0; i<round; i++)
        {
            int node = qu.front ();
            if (node == target)
                return shortest_step;
            // 將 vertex 所有的鄰居節點放入 queue
            for (neighbor:neightborhood)
            {
                if (visited[neightbor] == 0)
                {
                    qu.push (neighbor);
                    visited[neigbor] = 1;
                    prev[neighbor] = node;
                }
            }
            // 從 queue 中拿出節點，處理完就 pop
            qu.pop ();
        }
        shortest_step++;
    }
}

時間複雜度

最壞情況下，每個頂點都要進出 queue ，每個邊也都會被走訪一次，V 表示頂點個數， E 表示邊數，時間複雜度為 O (V+E) 。（對於連通圖來說，E 肯定要大於等於 V-1 ，所以其時間複雜度也可寫為 O(E) )

空間複雜度

消耗空間在於 3個用到的資料結構 : visited, prev 和 queue ，資料結構大小最大就是頂點個數的大小，所以空間複雜度為 O (V) 。

Leetcode #102 Binary Tree Level Order Traversal

最典型的 BFS 應用題，因為這題的圖是二元樹，並不會發生重複走訪到相同節點的問題，因此不需要使用到上述框架中的 visited 陣列。

vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector <int>> result;
        queue<TreeNode *> q;
        if (root != nullptr)
            q.push(root);
        while (!q.empty())
        {
            int qu_size = q.size();
            vector<int> level_vec;
            for (int i=0; i<qu_size; i++)
            {
                TreeNode *top_node = q.front();
                level_vec.push_back (top_node->val);
                if (top_node->left != nullptr)
                {
                    q.push (top_node->left);
                }
                if (top_node->right != nullptr)
                {
                    q.push (top_node->right);
                }
                q.pop();
            }
            result.push_back (level_vec);
        }

        return result;
    }

• 延伸練習 #111, #199

Leetcode #127 Word Ladder

這題要從一個單字，每次只能改變一個字元，問你最少轉換幾次才可以轉換到目標單字。

可以想像所有可能單字都是圖中的 vertex ，從起始單字開始，走到目標單字的最短路徑是我們要的答案，接下來思考一個問題，這張圖中究竟有多少點? 這些點是怎麼連接的呢？

以 h-i-t 這個單字來說，總共包含3個字元，每個字元都可以轉換為另外 26 個字母，轉換後的結果必須在 wordList 內，才能出現在圖上。

每轉換出一個新單字，需要做下列檢查：

1. 替換的字元不能跟未替換前一樣
2. 替換後如果是目標，直接回傳結果
3. 如果出現在 visited 內，直接忽略
4. 確認是否屬於 wordList 內的單字，不屬於裏面的單字不需要處理

優化

對於上述檢查第 3 點與第 4 點，還有值得優化之處。

在執行第 3 點檢查時，如果 wordList 內含許多單字狀況下，會遇到 Time Limit Exceeded 的狀況，等於每替換一次字元，就要把整個 wordList 掃過一輪去檢查替換後的單字是否在 wordList 內，時間複雜度太高。

更好的辦法是將 wordList 換成 unordered_set 來存放 ，透過 unoredered_set.find() 確認單字是否在 wordList 內，其時間複雜度僅 O(1) 。

這題有另外一個特別之處在於，可能出現在圖上的節點都被限定於題目給的 wordList 之中，每次遇到新節點，除了要檢查是不是已經走訪過，還要確定是否有出現在 wordList 中。
這邊可以做一個優化，將這兩項檢查做結合，每當轉變出一個新的單字，優先檢查該單字是否在 wordList 中，如果是就將該單字從 wordList 移除，這樣就可以保證不會再走訪到重複的單字了。

// 將 wordList 轉換為 unordered_set
unordered_set word_list (wordList.begin(), wordList.end());

// 每當有一個新的單字 curr ，先檢查 word_list 內是否有這個單字
if (word_list.count(curr))
{
    qu.push (curr);
    // 走訪過的單字由 word_list 中移除，避免重複走訪
    word_list.erase(curr);
}

這題完整的程式碼如下：

class Solution {
public:
    int ladderLength(string beginWord, string endWord,
                        vector<string>& wordList)
    {
        unordered_set<string> path (wordList.begin (),
                                    wordList.end ());
        if (path.find (endWord) == path.end ())
            return 0;

        queue<string> qu;
        qu.push (beginWord);
        int step = 0;

        while (!qu.empty ())
        {
            step++;
            int todo = qu.size ();
            for (int i=0; i<todo; i++)
            {
                string curr = qu.front ();
                qu.pop ();

                // iterate each char of string
                for (int idx=0; idx<curr.size (); idx++)
                {
                    string replaceCurr = curr;
                    // change character from a to z
                    for (int ch='a'; ch<='z'; ch++)
                    {
                        replaceCurr[idx] = ch;
                        if (replaceCurr == endWord)
                        {
                            return step+1;
                        }
                        if (replaceCurr == curr)
                            continue;
                        if (path.find (replaceCurr)
                                    != path.end())
                        {
                            qu.push (replaceCurr);
                            path.erase (replaceCurr);
                        }
                    }
                }
            }
        }
        return 0;
    }
};

時間複雜度

以 M 代表單字的長度， N 代表 wordList 內單字數量。
最壞情況下 N 個可能單字都遇到，每個單字有 M 個字母，總共有 MxN 種組合，每種組合要再存成一個新單字 ，又需要 O(M) ，總共時間複雜度為 O(M^2 x N) 。

空間複雜度

最多需要 O (M x N) 來儲存所有可能單字。

參考資料

1. Breadth First Search or BFS for a Graph
2. 14 Patterns to Ace Any Coding Interview Question by @fahimulhaq
3. BFS 算法解题套路框架

Updated on 2022-04-16 22:47:45 星期六