Linked List 的反轉操作 – 陪你刷題

在做 linked list 相關題目時，不論是 recursive 還是 iterative 寫法，寫起來都相當燒腦，因此決定以自己好理解的方式，整理一篇跟 linked list 反轉操作的文章，作為往後複習來用。

Leetcode #206 Reverse Linked List

遞迴寫法

在開始透過遞迴的方式來反轉 linked list 之前 ，先回想如何才能使用遞迴，使用遞迴需要滿足以下 3 個條件：

  1. 一個問題的解可以分為幾個子問題的解
  2. 這個問題和其子問題除了數據規模不同，求解思路完全一樣
  3. 存在遞迴終止條件 (base case)

在思考遞迴問題時，很重要的一點是，絕對不要在腦中想把遞迴一層一層的想清楚，這不符合一般人腦的思考方式！

單純聚焦於反轉過程中的某一子問題，可以幫助我們思考清楚整個遞迴，如下圖，如果反轉完 head→next ，接著該怎麼反轉 head 呢？

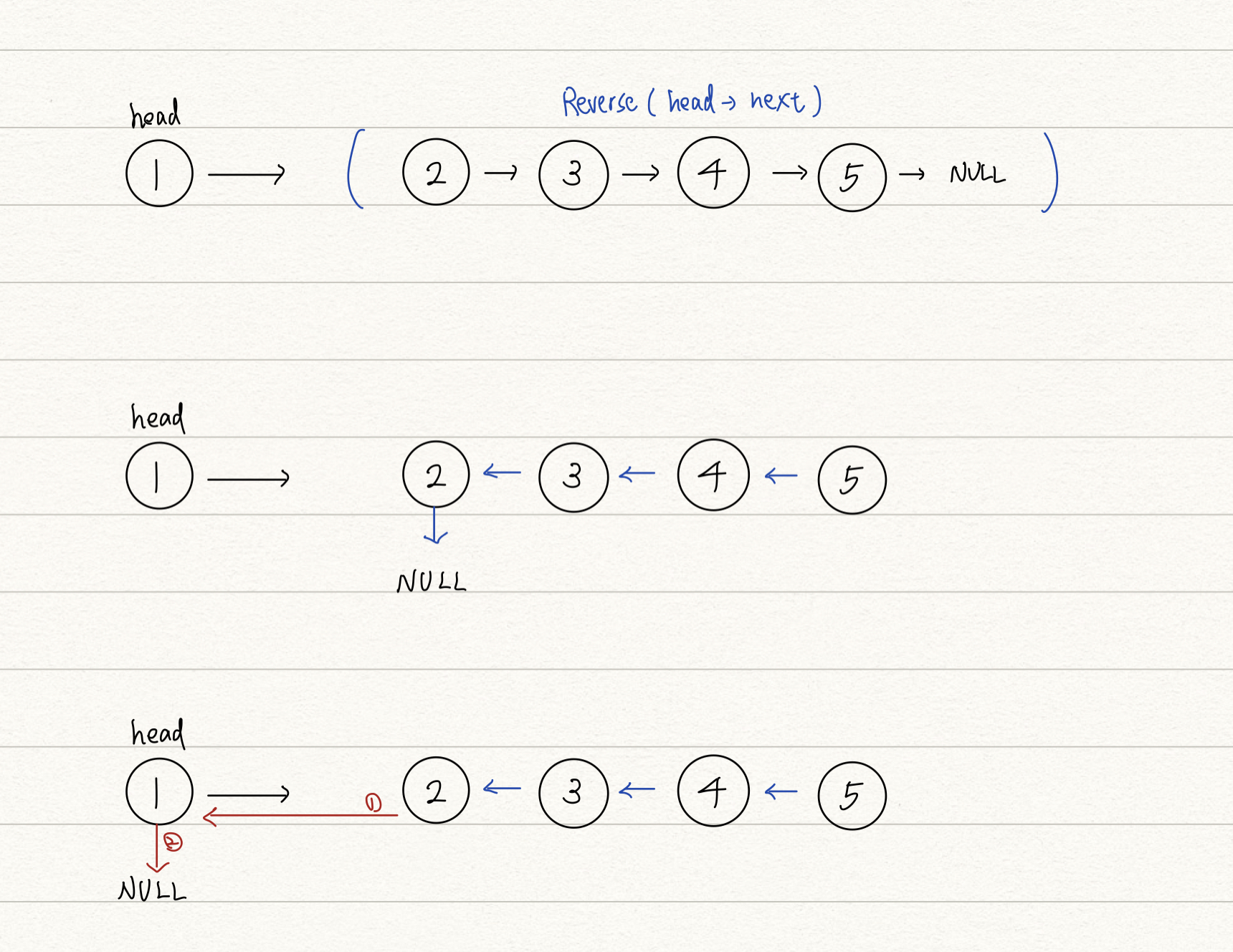
LinkedlistReverse

第一步將 head→next 接往 head 做到反轉：

head->next->next = head;

第二步將 head→next 指到 nullptr ，至此 head 節點的前後都被正確反轉。

head->next = nullptr;

遞迴問題中，必須定義出終止條件，以反轉 linked list 來說，當走到最後一個節點時後，該節點就不需要再往後處理，而這個節點就會是新的 head 節點，直接回傳即可。

掌握以上要點後，遞迴的程式碼也就可以輕鬆寫出。

ListNode *reverseList (ListNode *head)
{
    if (head == nullptr || head->next == nullptr)
        return head;
    ListNode *new_head = reverseList (head->next);
    head->next->next = head;
    head->next = nullptr;
    return new_head;
}

非遞迴寫法

專注於當前節點的反轉即可。

演算法如下:

  1. 定義兩個指針 prev 和 next 。prev 最終將指向反轉後鏈表的頭節點，初始化為 nullptr。
  2. 使用 while 迴圈遍歷原本的 linked list， 每次迭代取得當前節點 curr。
  3. 將 next 指向 curr 的下一個節點，保存當前節點的下一個節點。
  4. 將 curr->next 指向 prev，實現反轉操作。
  5. 將 prev 指針移到當前節點 curr ，curr 移到下一個節點 next。
  6. 重複步驟 2-5，直到遍歷完原本的 linked list。
  7. 最後 prev 指向的是反轉後新的頭節點。
class Solution {
public:
    ListNode* reverseList(ListNode* head) {

        ListNode *prev = nullptr;
        ListNode *curr = head;
        while (curr != nullptr)
        {
            ListNode *next = curr->next;
            curr->next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
};

Leetcode #92 Reverse Linked List II

此題的 input 給你 [m, n] 的區間，要你 reverse 特定區間內的節點，以下分為遞迴與非遞迴的寫法。

遞迴寫法

我們先從如何 reverse 前 N 個節點開始了解。

Reverse 前 N 個節點

與 reverse 整個 linked list 差別在於：

  1. 必須將反轉過後的 linked list 的尾節點 （圖中的 new_tail 或反轉前的 head ） 接往第 N+1 個節點 （圖中的 successor 或者你要說它是反轉區間最後節點的下一個節點），之前 reverse 整個 linked list 時候，會將當前的節點的 next 指向 NULL ，但這個 case 下要將當前節點指向第 N+1 的節點。

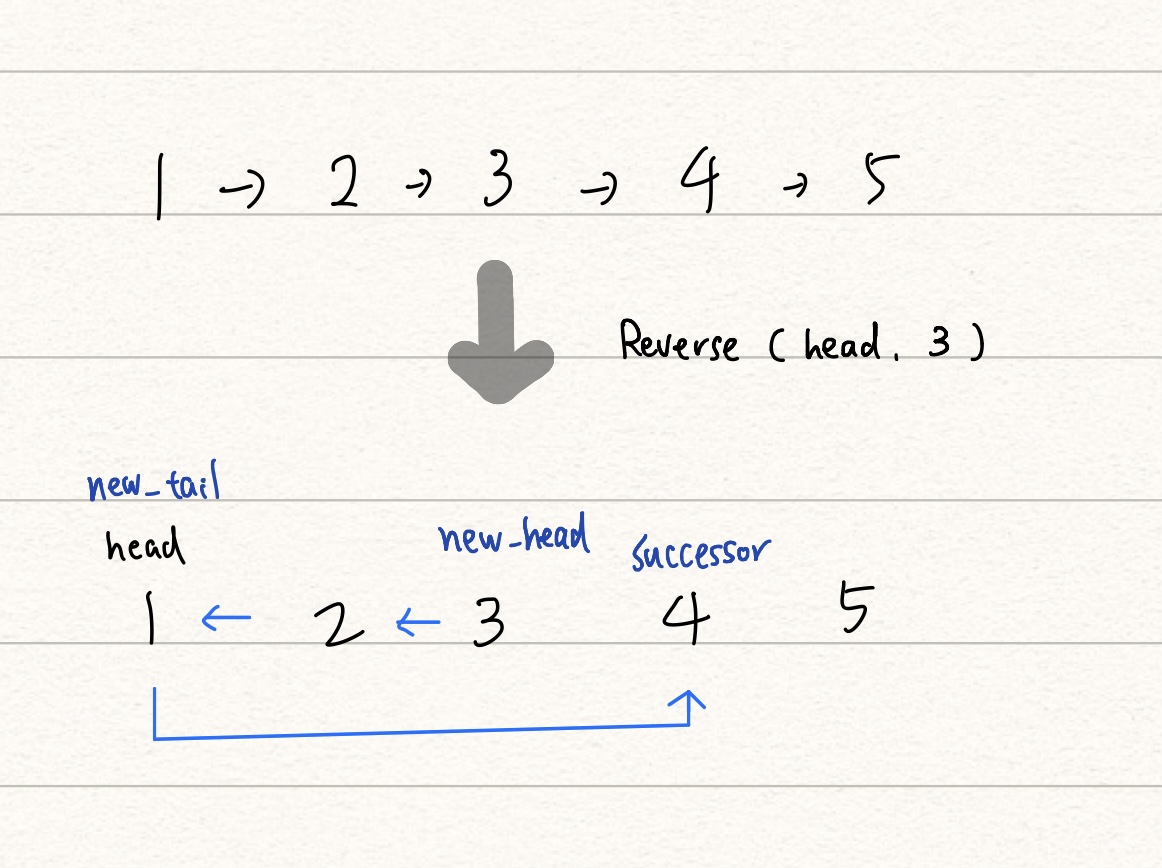
reverseN

遞迴的中止條件為當 n=1 的時候，代表不必再反轉後續節點，但要將第 N+1 個節點紀錄下來，並且回傳新的頭節點。

ListNode *successor = nullptr;

ListNode *reverseN (ListNode* head, int n)
{
    if (n == 1)
    {
        successor = head->next;
        return head;
    }
    ListNode *new_head = reverseN (head->next, n-1);
    head->next->next = head;
    head->next = successor;
    return new_head;
}

反轉特定區間節點

知道如何 reverse 前 N 個節點後，其實 reverse 區間 [m, n] 的節點，等同於我們先前進到第 m 個節點，就以第 m 個節點開始來 reverse (n-m) 個節點即可。

透過遞迴來實作的話，遞迴中止條件即為 m = 1 的時候，回傳反轉後的新頭節點，其他的 case 下直接將節點一個一個走下去，更新區間的開頭與結束 index 即可。

ListNode* reverseBetween (ListNode *head, int m, int n)
{
    if ( m == 1)
    {
        return reverseN (head->next, n);
    }
    head->next = reverseBetween (head->next, m-1, n-1);
    return head;
}

非遞迴寫法

相比於遞迴寫法，非遞迴更加複雜。以下圖為例，可以觀察到兩個現象：

  1. 反轉區間的前一個節點永遠接往新的頭節點（圖中的 new_head )
  2. 反轉過後的 linked list 的尾節點 （圖中的 new_tail ）接往反轉區間的後一個節點

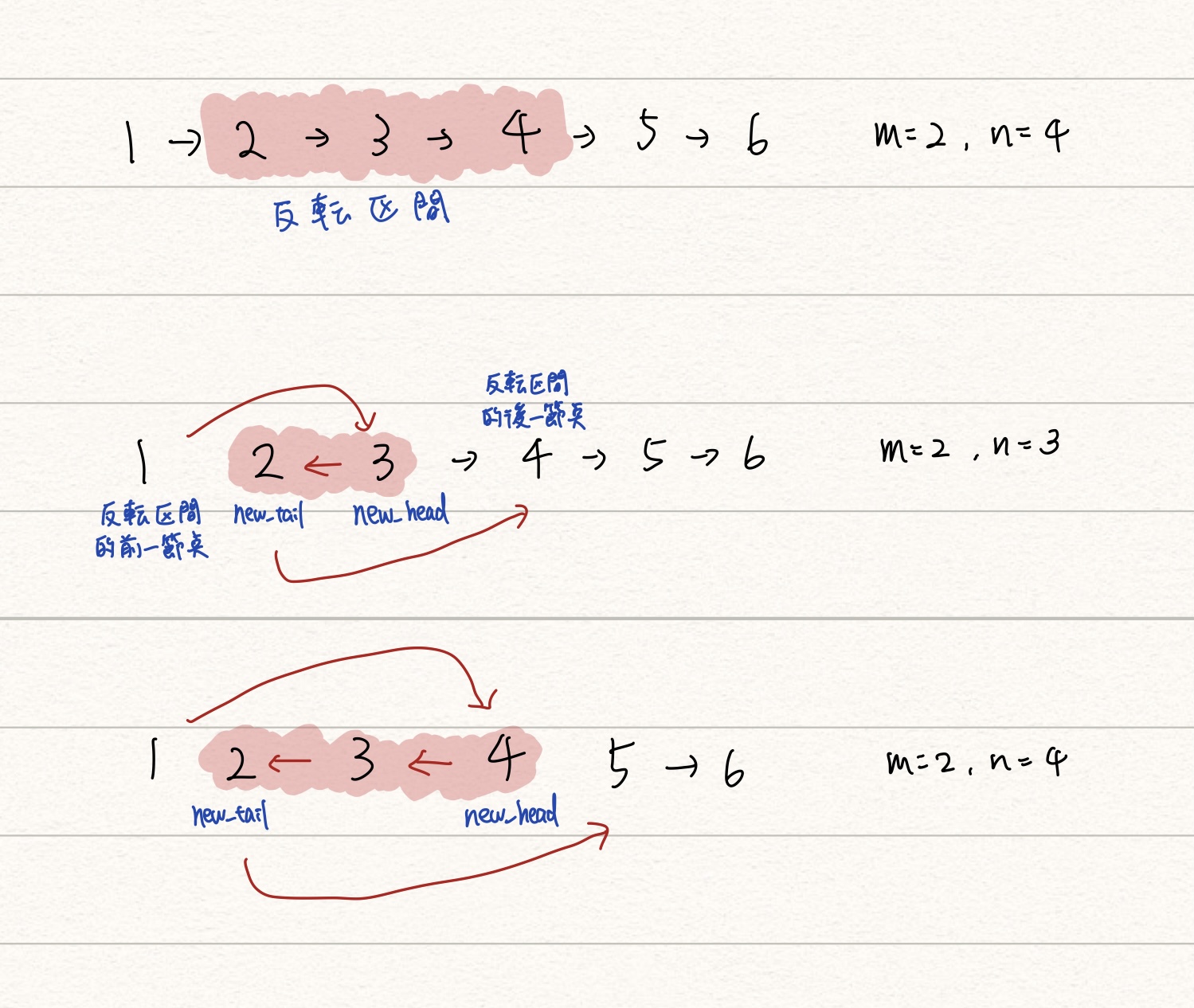
只要在每次反轉時把握兩個現象正確，再搭配反轉動作，就可以正確完成反轉區間的任務。總結一下，每次 反轉都會做到以下三樣任務：

  1. 反轉區間的前一個節點永遠接往新的頭節點（圖中的 new_head )
  2. 反轉過後的 linked list 的尾節點 （圖中的 new_tail ）接往反轉區間的後一個節點
  3. 反轉兩個節點

另外提一下，這邊使用哨兵節點來處理會更好，可以避免需要特別處理 m=1 時的特殊狀況。

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        ListNode *dummy = new ListNode(0), *pre = dummy;
        dummy -> next = head;

        for (int i = 0; i < m - 1; i++) {
            pre = pre -> next;
        }
        ListNode *new_tail = pre -> next;

        for (int i = 0; i < n - m; i++) {
                // 將上一輪的頭節點存下來
                ListNode* temp = pre -> next;
                // 現象 1
                pre -> next = new_tail -> next;
                // 現象 2
                new_tail -> next = new_tail -> next -> next;
                // 新一輪的頭節點接往上一輪的頭節點
                pre -> next -> next = temp;
            }
            return dummy -> next;
        }
};

這 3 個任務並沒有一定的先後順序，只要確保每個動作執行完後，所有節點都不會變成孤兒就可以了，以下提供另外一種實作， walker 指標用來走訪反轉區間，他走到哪就要反轉到哪。

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        if (head == nullptr || head->next == nullptr)
            return head;
        if (m==n)
            return head;

        ListNode *dummy = new ListNode(0), *prev = dummy;
        dummy->next = head;

        for (int i=1; i<m; i++)
        {
            prev = prev->next;
        }
        ListNode *new_tail = prev->next;
        ListNode *walker = new_tail->next;

        for (int i=m; i<n; i++)
        {
            new_tail->next = walker->next;
            walker->next = prev->next;
            prev->next = walker;
            walker = new_tail->next;
        }
        return dummy->next;
    }
};

Leetcode #25 Reverse Nodes in k-Group

每 k 個節點為一個 group 進行反轉。

遞迴寫法

這題可以視為 #92 的進階題。

  1. 每次都先走 k 步確認有足夠多的數量可以進行反轉。
  2. 進行反轉後需要將新的 head 節點回傳回去，以利接起整個 linked list 。
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if (k==1)
            return head;

        ListNode *walker = head;
        for (int i = 0; i<k; i++)
        {
            if (walker != nullptr)
            {
                walker = walker->next;
            }
            else
            {
                // If number of left nodes is smaller than k, just return.
                return head;
            }
        }

        ListNode *new_head = reverseN (head, k);
        head->next = reverseKGroup (walker, k);

        return new_head;
    }
private:
    ListNode *successor = NULL;
    ListNode* reverseN (ListNode *head, int k)
    {
        if (k==1)
        {
            successor = head->next;
            return head;
        }
        ListNode *new_head = reverseN (head->next, k-1);
        head->next->next = head;
        head->next = successor;
        return new_head;
    }
};

非遞迴寫法

主要分為兩步驟：

  1. 先走訪整個 list 找出 list 的總長度。
  2. 透過 for loop 依序 swap 每個 group ，已經知道 list 的總長度，就可以控制總共要 swap 多少個 group 。

延伸練習

結論

在處理 linked list 問題時，最重要一點就是不要讓任何節點變成孤兒，了解題目後，把題目需要的操作列出來，確認都有執行且執行過程不會讓任何節點變為孤兒，那就可以放心透過遞迴或是 iterative 的模式操作。

Updated on 2023-09-28 22:33:49 星期四

發佈留言

發佈留言必須填寫的電子郵件地址不會公開。 必填欄位標示為 *