Leetcode 邁向千題的關卡，想要把所有題目刷過一遍，對於一位上班族來說就跟寫出來的程式沒有 bug 一樣困難，因此想要將刷題常用的觀念技巧與其對應題目整理出來，一方面可以整理自己思緒，也可以做為未來複習用。
這系列文章會一直持續下去，算是作為工程師職涯的隨身裝備。

如何辨識 Topological 類型題目

1. 資料間的先後關係：給你一組資料，資料之間存在先後關係（例如：元素 A 一定要先於元素 B），要你排出所有資料的線性排序。 具體的應用就是課程檔修，想要修資料結構，一定要先修過基礎程式設計。
2. 找出有向圖中的 cycle：如果圖中存在環 (cycle)，則無法成功進行 topological sort。這是因為環中的元素無法確定一個線性的先後順序。

何謂 Topological Sort

Topological Sort 是針對有向無環圖（Directed Acyclic Graph，簡稱 DAG）中的頂點排序，使得對於每一條邊 (u, v)，頂點 u 都排在頂點 v 的前面。這意味著，如果存在一條邊從頂點 u 指向頂點 v，則 u 必須在 v 之前出現在排序中。
另外，Topological Sort 產生的線性排序並不是唯一的，可能有多種排序方式。
例如下圖中這個例子，我相信你一定可以寫出跟我不一樣的 topological sort 結果。

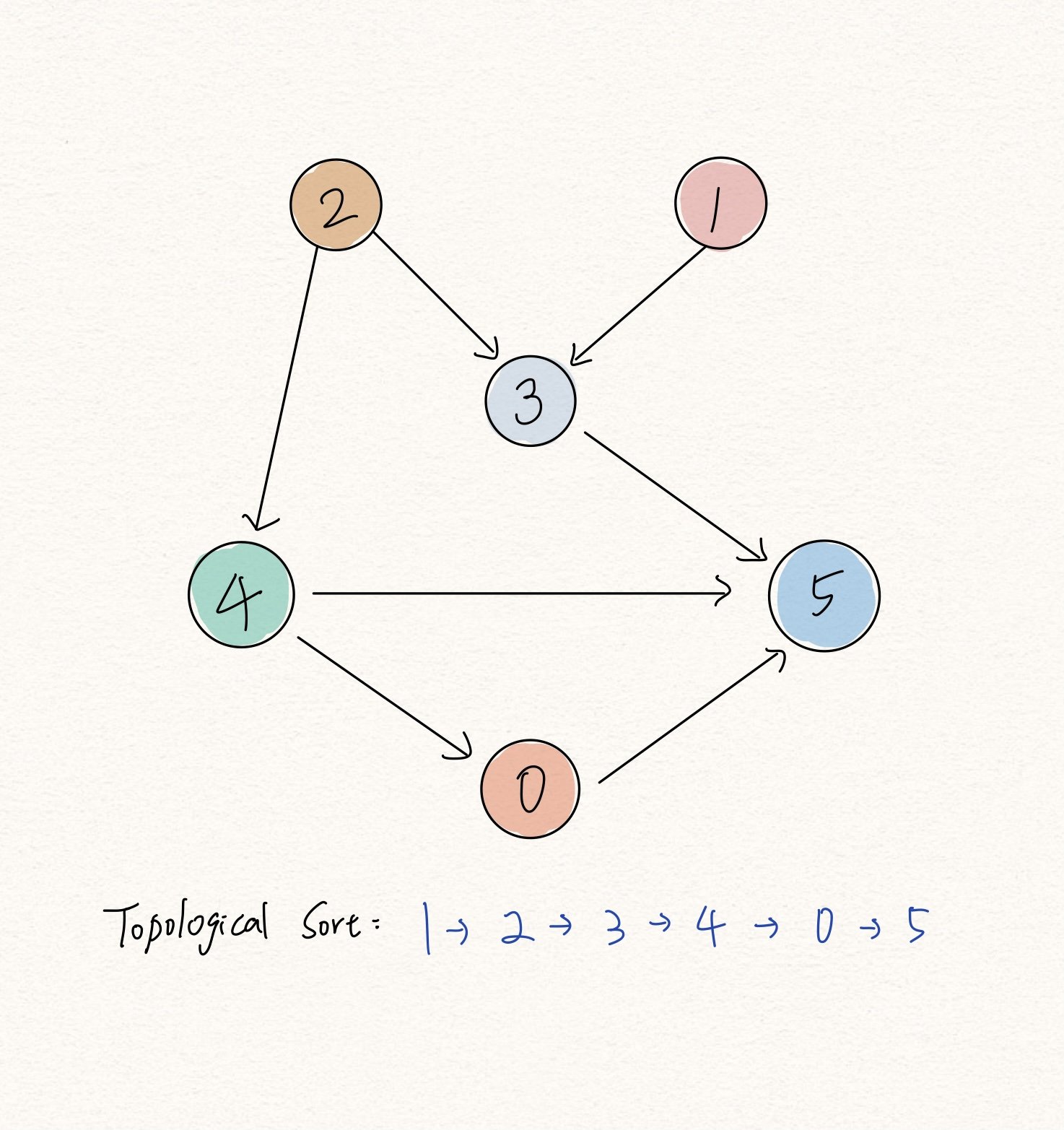
Leetcode#207 Course Schedule

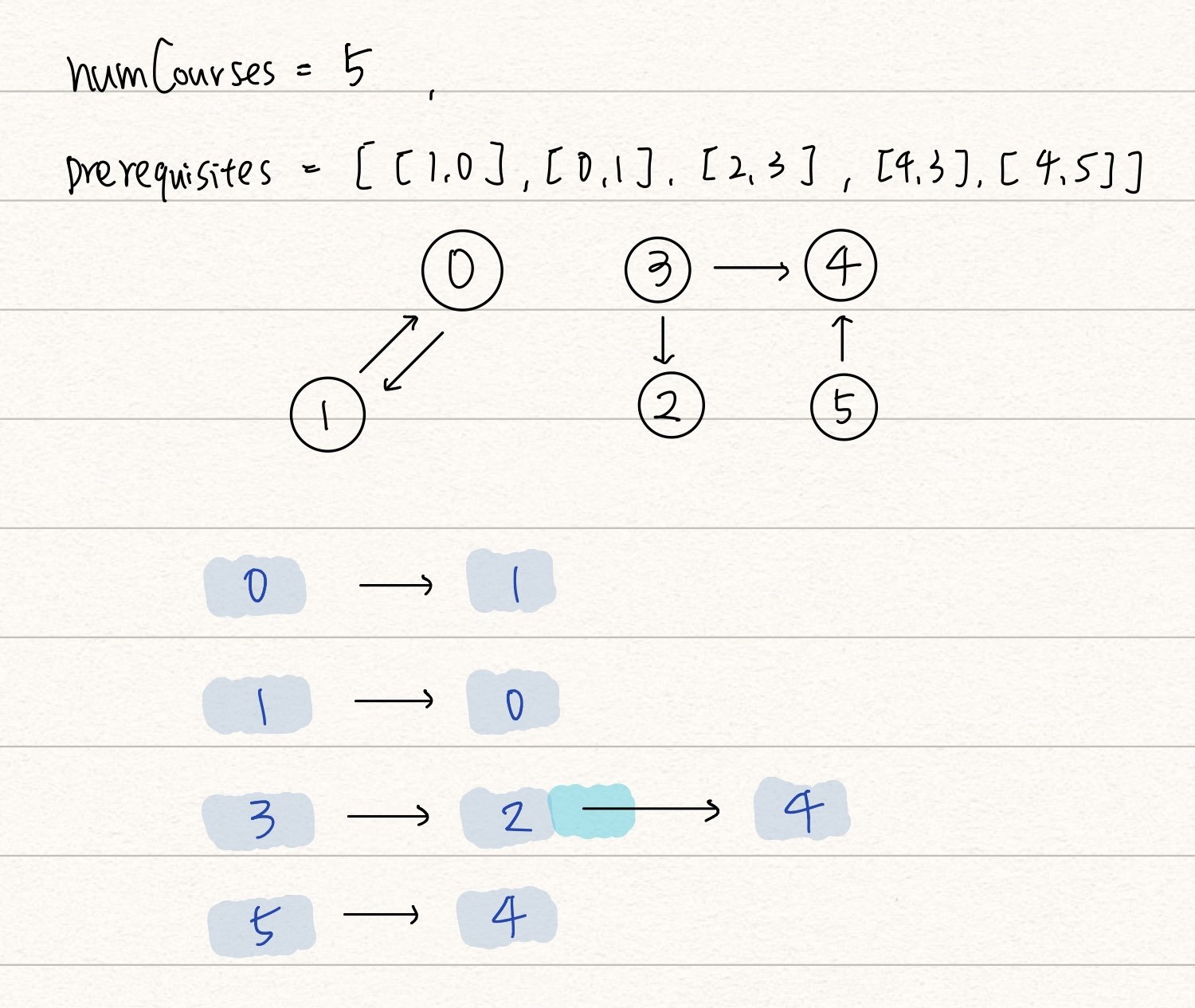
題目給你課程數量與各課程的先修課（例如要修大二的資料結構，就必須要先修過大一的程式設計課），問你會不會發生無法成功修課的情況？

如果課程之間環環相依，就會造成無法修課的情況，透過有向圖來表達課程的相依關係，可以觀察到無法修課的情況發生時，代表圖中存在 cycle ，所以此題也等同於問你圖內是否存在 cycle 。

解法 1 Backtracking

建議可以先看之前寫的 backtracking 回溯法 - 陪你刷題

1. 先建 graph

• 以 adjacent list 方式來表達圖

// Build graph
vector<vector<int>> courseDict;
for (int i=0; i<prerequisites.size(); i++)
{
    courseDict[prerequisites[i][0]].push_back(prerequisites[i][1]);
}

這邊若使用 unordered_map ，在課程數量達到 1000 時，會 Time Limit Exceeded 。
unordered_map 的底層為紅黑樹，比較適合需要 hash table 場景時使用; vector 則是以一塊連續記憶體來儲存，在存取資料會更快，所以當你知道資料 index 範圍時， vector 會是比較好的選擇。

2. 走訪整個圖去檢查是否存在 cycle

把整個圖都走訪過一遍，就可以知道是否存在 cycle 。 想要遍歷整個圖，可以想到使用 Backtracking 演算法。

透過 backtracking 來將所有可能的路徑走過，利用 array 來紀錄曾經拜訪過哪個點，如果再次遇到已經拜訪過的點，代表找到 cycle 。

Backtracking 是以遞迴形式實作，（延伸閱讀：Backtracking - 陪你刷題）需要定義 base case ，有以下兩種：

1. 遇到已經拜訪過的節點，那就代表找到 cycle ，直接回傳 true
2. 該路徑後面已經無路可走了，直接回傳 false

程式碼

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        // Build graph
        vector<vector<int>> courseDict(numCourses);
        for (int i=0; i<prerequisites.size(); i++)
        {
            courseDict[prerequisites[i][0]].push_back(prerequisites[i][1]);
        }
        vector<bool> visit (numCourses, false);
        // Iterate each node. If there is any cycle, return false
        for (int i=0; i<numCourses; i++)
        {
            if (isCycle (i, courseDict, visit))
            {
                return false;
            }
        }
        return true;
    }
private:
    bool isCycle (int courseNum, vector<vector<int>>& courseDict,
                    vector<bool>& visited)
    {
        if (visited[courseNum])
            return true;
        int nextSize = courseDict[courseNum].size();
        if (nextSize == 0)
            return false;

        visited[courseNum] = true;

        for (int i=0; i<nextSize; i++)
        {
            if (isCycle (courseDict[courseNum][i],
                    courseDict, visited))
            {
                return true;
            }
        }

        visited[courseNum] = false;
        return false;
    }
};

時間複雜度

以 E 代表 prerequisites (課程相依關係) 的數量，以 V 代表課程總數。

建圖的過程需要耗費 O(E) ，接下來依序以每個點為起點開始，檢查是否有 cycle ，最遭的情況下可能每個起點開始都要走完所有的點，因此需要耗費 O (V^2) ，總和的時間複雜度要 O ( E + V^2 ) 。

空間複雜度

• 建圖就需要 O (V + E) 空間
• 製圖需耗費 O (E) 。
• 在 backtracking 的遞迴過程中，最多會遞迴 V 層，因此需要 O (V) 空間
• 紀錄是否走訪過節點的 array 會需要 O(V) 空間

方法 2 backtracking 應用剪枝技巧

觀察方法 1，很多的路徑都被重複檢查，那麼能不能夠每條路徑檢查一遍就好呢？ 答案是可以的。

假設以某點為起點的所有路徑如果都不存在 cycle ，那在這個起點之前再加入任何的點，也不會因此形成 cycle 。

也就是說一條路徑在某次檢查中已經確認沒有 cycle 了，那麼下次再走到這條路徑，不需要再檢查下去了，可以直接宣稱以他為起點的路徑不存在 cycle 。

基於方法 1 的實作，只需要再一個 array 來紀錄該點為起點的路徑是否已經檢查過，在 backtracking 的 base case 中，再新增一點：

• 一旦以該點為起點的路徑都不存在 cycle ，就不用再往下檢查，直接回傳 false

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        // Build graph
        vector<vector<int>> courseDict(numCourses);
        for (int i=0; i<prerequisites.size(); i++)
        {
            courseDict[prerequisites[i][0]].push_back(prerequisites[i][1]);
        }
        vector<bool> visit (numCourses, false);
        vector<bool> check (numCourses, false);
        // Iterate each node. If there is any cycle, return false
        for (int i=0; i<numCourses; i++)
        {
            if (isCycle (i, courseDict, visit, check))
            {
                return false;
            }
        }
        return true;
    }
private:
    bool isCycle (int courseNum, vector<vector<int>>& courseDict,
                  vector<bool>& visited, vector<bool>& checked)
    {
        // base case
        if (checked[courseNum])
            return false;
        if (visited[courseNum])
            return true;
        int nextSize = courseDict[courseNum].size();
        if (nextSize == 0)
            return false;

        visited[courseNum] = true;

        for (int i=0; i<nextSize; i++)
        {
            if (isCycle (courseDict[courseNum][i], courseDict,
                                            visited, checked))
            {
                return true;
            }
        }

        visited[courseNum] = false;
        checked[courseNum] = true;
        return false;
    }
};

時間複雜度

以 E 代表 prerequisites (課程相依關係) 的數量，以 V 代表課程總數。

建圖需要 O (E) 的時間，而走訪圖的部份，就如同以 DFS 形式走訪圖，共需要 O (V+E) 的時間。

空間複雜度

• 建圖就需要 O (V + E) 空間
• 在 backtracking 的遞迴過程中，最多會遞迴 V 層，因此需要 O (V) 空間
• 需要兩個 array 紀錄，共 O(2V) 空間

看到這邊，千萬不要去記，

以後看到 topological sort 類型題目，就想到可以把整張圖都遍歷來確認是否存在 cycle ，遍歷整張圖可以想到 backtracking 。

請試圖去理解為什麼用這樣的方法，想要確認圖中是否有 cycle ，直覺想法一定是那就每個點開始走走看，如果存在 cycle 代表你會走到重複的點，
而從每個點開始走走看，這樣的動作以程式碼來實現，自然想到 DFS ，DFS 背後的思想就是回溯法。

方法 3 Topological Sort - Kahn's algorithm

透過 topological sort 檢查圖中是否存在 cycle ，其步驟為：

1. 計算所有點的 in-degree (進入該點的邊數量）。
2. 將 in-degree 為 0 的點放入 queue 。
3. 從 queue 中拿出頂點，並執行以下步驟
   1. 利用一個變數紀錄 dequeue 的節點數，每拿出一個點，就將變數加 1
   2. 將該頂點的鄰節點 in-degree 減 1 ，因為接往他的節點要被移除掉了
   3. 如果有鄰節點的 in-degree 已經歸零，將他放入 queue
4. 重複步驟 3 直到 queue 為空。
5. 檢查 dequeue 的數量是否等於節點總數 （如果存在 cycle 的話，cycle 路徑上的節點 in-degree 是永遠都無法歸零的）

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        // Build graph
        vector<vector<int>> courseDict(numCourses);
        vector<int> inDegree(numCourses, 0);
        for (int i=0; i<prerequisites.size(); i++)
        {
            int prev = prerequisites[i][1];
            int curr = prerequisites[i][0];
            courseDict[prev].push_back(curr);
            inDegree[curr]++;
        }

        queue<int> start;
        int dequeueNum = 0;

        for (int i=0; i<numCourses; i++)
        {
            if (inDegree[i]==0)
            {
                start.push(i);
            }
        }

        while (!start.empty())
        {
            int node_index = start.front();
            dequeueNum++;
            start.pop();
            for (int i=0; i<courseDict[node_index].size(); i++)
            {
                inDegree[courseDict[node_index][i]]--;
                if (inDegree[courseDict[node_index][i]] == 0)
                {
                    start.push (courseDict[node_index][i]);
                }
            }
        }
        return dequeueNum == numCourses;
    }
};

時間複雜度

以 E 代表 prerequisites (課程相依關係) 的數量，以 V 代表課程總數。

建圖需要 O (E) 的時間，而走訪圖的部份，就如同以 DFS 形式走訪圖，共需要 O (V+E) 的時間。

空間複雜度

• 建圖就需要 O (V + E) 空間
• queue 會消耗 O (V) 空間

千萬不要去記可以用 Kahn's algorithm ，這個演算法每個步驟各是什麼，這並不是正確學習方式，試著去理解演算法每個步驟的意義，特別推薦去看 CTCI 針對問題 4.7 答案的推導過程，這才是正確的學習方式。 這邊再多說一點的是，不知道你有沒有發現，Kahn's algorithm 本身是一種 BFS 來 traverse graph 的作法 ，BFS 遍歷的順序，也是 topological sort 的結果。

延伸練習

• Leetcode #210, #269, #444

總結

Topological Sort 在 Leetcode 中的題目雖然不多，但出現頻率高。了解三種常見解法（Backtracking、改進的 Backtracking 和 Kahn's Algorithm），並理解其內在意義，比僅記住步驟更為重要。希望這篇文章能幫助你更好地理解和掌握 Topological Sort 的相關知識。

Reference

1. 14 Patterns to Ace Any Coding Interview Question

Updated on 2022-06-18 20:51:03 星期六