Merge Interval 技巧可以有效解決 Overlapping intervals 的問題，這類問題可以衍生為找出 overlapping intervals 或是將 overlapping intervals 合併在一起，解決這類問題前，先歸納出區間之間關係，共有下圖六種狀況：

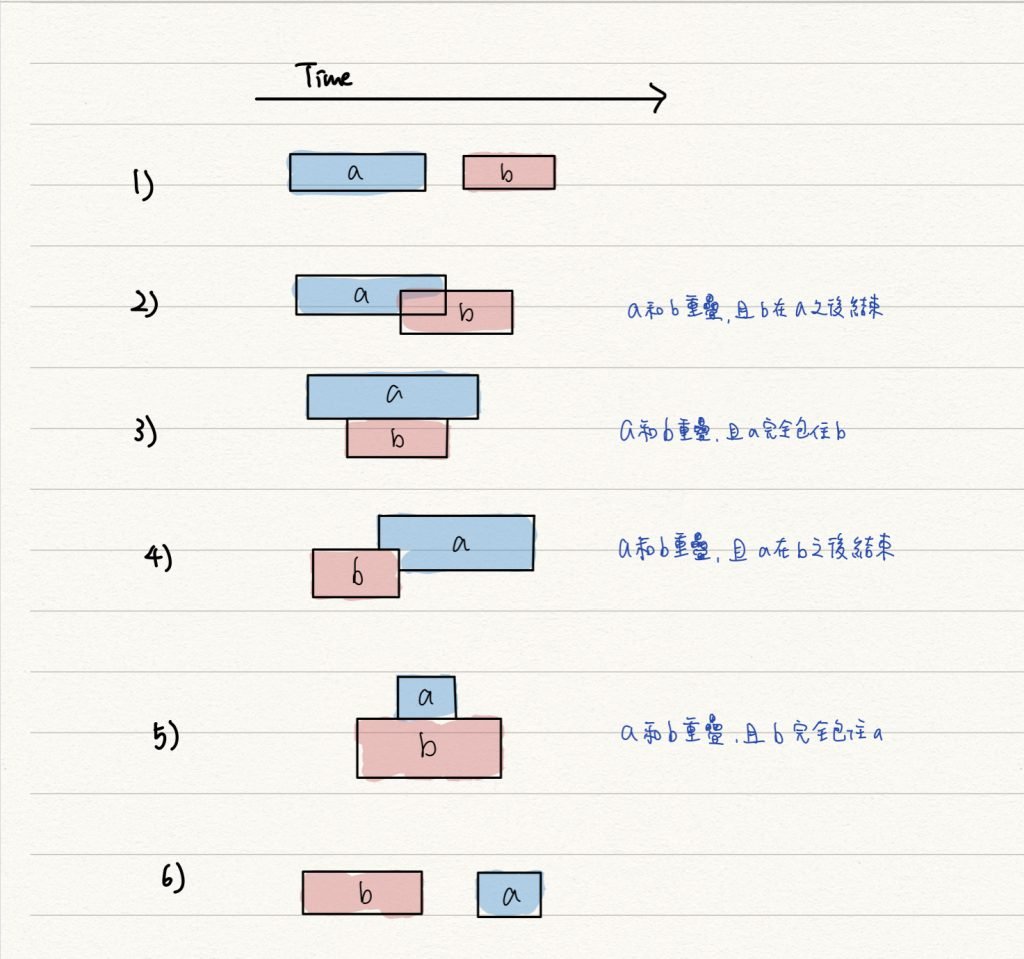
圖中的 case 2 ~ 4 符合要做區間合併的條件，由此可以了解，如果 a 和 b 區間要合併必定滿足兩個條件:

1. b 區間的起點 < a 區間的終點
2. b 區間的終點 > a 區間的起點

遇到 interval 問題時，兩個 interval 之間關係脫不了上圖中的六種狀況，若你需要合併區間，可以透過畫圖方式確認哪種狀況需要合併，合併後區間的起點跟終點大小該怎麼定。

Leetcode #056 Merge Intervals

演算法：

1. 依照區間起點大小來排序所有區間。
2. 如何判斷兩個區間是否該合併? 依照區間起點排序後，兩個區間的關係只剩下如下圖中 3 種可能性，僅後 2 種 case 需要合併，符合 B 區間的起點小於 A 區間的終點的條件。

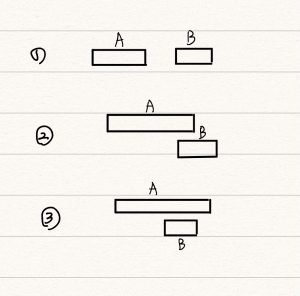
3. 合併後區間的起點跟 end 該如何決定？
   由於按照起點來排序所有的區間了，所以合併區間的起點必定是 A 區間的起點 ，而合併區間的終點則由兩區間的終點的最大值來決定 （對照上圖的後兩種狀況）。

class Solution {
public:
    static bool interval_sort () (vector<int>a, vector<int>b) {
         return a[0] < b[0];
    }
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        std::sort (intervals.begin (), intervals.end(), interval_sort);

        vector<vector<int>> result;
        for (int i=0; i<intervals.size(); i++)
        {
            if (result.size() == 0 ||
               result.back()[1] < intervals[i][0])
            {
                result.push_back (intervals[i]);
            }
            else
            {
                result.back()[1] =
                    std::max (result.back()[1], intervals[i][1]);
            }
        }
        return result;
    }
};

時間複雜度

O (n log n)

空間複雜度

O (n)

延伸練習

Leetcode #616, #763

Leetcode #057 Insert Interval

暴力法

直接將 newInterval 加入區間組，再對區間組排序，就等同 Leetcode #56 ，時間複雜度為 O(n log n)。

方法 2

原始 intervals 已經排序過，這是一個很重要的前提，應該充分利用，避免像方法 1 一樣做多餘的排序。

遇到 merge interval 類型問題，最煩人的就是要處理各種不同狀況，千萬不要在腦海中自己思考，直接畫圖會是最好的方式，根據下圖，區間與 newInterval 存在 4 種狀況，依序處理這 4 種狀況即可：

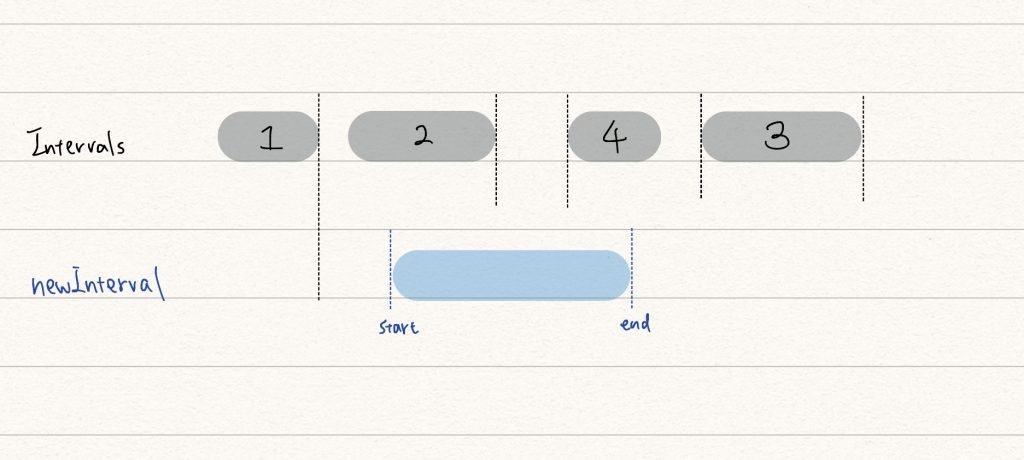
1. 第一種狀況如同 newInterval 和 1 號區間的關係，newInterval 的起點大於 1 號區間的終點 ，不需要 merge 。
2. 不屬於第一種狀況，代表 newInterval 的起點小於接下來的區間的終點 ，上圖的 2 號, 3 號 跟 4 號區間均符合條件。但僅有 2 跟 4 號需要合併，關鍵條件在於，newInterval 的終點有大於區間的起點 ，就需要做 merge 。
3. 接下來的區間的起點均大於 newInterval 的終點 (如同上圖的 3 號區間)，不需要做 merge 。

將以上四個不同狀況翻譯為程式碼，即可順利解決這類問題。

class Solution {
public:
    vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
        vector<vector<int>> result;
        int index = 0;

        if (intervals.size () == 0)
        {
            intervals.push_back(newInterval);
            return intervals;
        }
        if (newInterval[0] > intervals.back()[1])
        {
            intervals.push_back(newInterval);
            return intervals;
        }

        // Step 1
        while (index < intervals.size() && 
               intervals[index][1] < newInterval[0])
        {
            result.push_back (intervals[index]);
            index++;
        }
        // Step 2
        while (index < intervals.size() &&
               intervals[index][0] <= newInterval[1])
        {
            newInterval[0] =
                std::min (newInterval[0], intervals[index][0]);
            newInterval[1] =
                std::max (newInterval[1], intervals[index][1]);
            index++;
        }
        result.push_back (newInterval);
        // Step 3
        while (index < intervals.size())
        {
            result.push_back (intervals[index]);
            index++;
        }
        return result;
    }
};

時間 & 空間複雜度

均為 O (n) 。

延伸練習

Leetcode #253

結論

碰到這類問題，不需要在腦海中想出所有排列可能性，所有情況都不出第一張圖的六種，冷靜的分析搭配畫圖，就能輕鬆解決這類型題目。
有一點我想要特別分享，我在前篇寫了 Interval Scheduling – 陪你刷題 ，接著馬上寫下本篇介紹 merge intervals ，原因是我在一開始接觸這兩類型題目時，常常搞混他們，甚至覺得這兩種類型題目都屬於同一種，但寫下這兩篇後，我有一個深刻的認知來分辨這兩種類型，Interval scheduling 背後的中心思想是 greedy algorithm ，而 Merge Intervals 背後的中心思想，則是排序陣列並依照區間之間的關係做處理，兩者使用的是截然不同的技巧。

Reference

1. 14 Patterns to Ace Any Coding Interview Question

Updated on 2024-03-17 19:52:45 星期日