Leetcode 邁向千題的關卡，想要把所有題目刷過一遍，對於一位上班族來說就跟寫出來的程式沒有 bug 一樣困難，因此想要將刷題常用的觀念技巧與其對應題目整理出來，一方面可以整理自己思緒，也可以做為未來複習用。 這系列文章會一直持續下去，算是作為工程師職涯的隨身裝備。

透過此篇你可以學習到什麼？

詳解三種 binary tree 的走訪，並且以遞迴或非遞迴的方式實現。

逐一走訪樹的每個節點

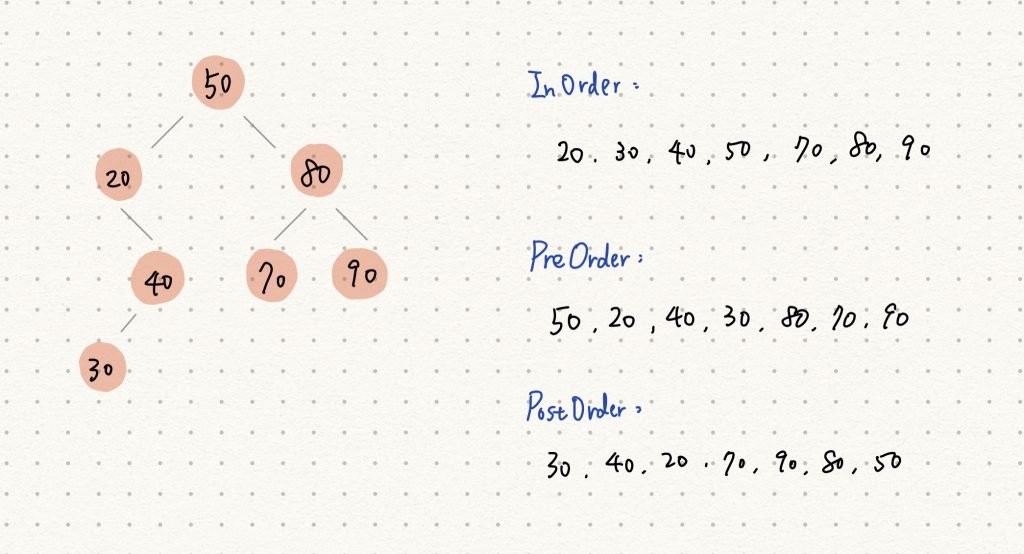
透過下圖來理解三種 tree traversal 的走訪先後順序：

1. In-order Traversal (中序遍歷）：左子樹 → root → 右子樹
2. Pre-order Traversal (前序遍歷）：root → 左子樹 → 右子樹
3. Post-order Traversal (後序遍歷）：左子樹 → 右子樹 → root

我是怎麼記得這個順序的呢？
前序遍歷，可以想成造訪子節點 "前" 造訪目前節點，後序遍歷想成造訪子節點 "後" 造訪目前節點。

中序遍歷

遞迴作法

透過遞迴方式來實作是相當簡單，以下直接展示程式碼：

class Solution {

public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        inorderHelper (root, result);
        return result;
    }
private:
    void inorderHelper (TreeNode *root, vector<int> &result)
    {
        if (root == nullptr)
            return;
        inorderHelper(root->left, result);
        result.push_back (root->val);
        inorderHelper(root->right, result);
    }
};

時間複雜度

O (n) 。 因為遞迴方程式的時間複雜度為 T(n) = 2 T(n/2) + 1 。

空間複雜度

最糟糕空間複雜度為 O(n) ，平均可以到 O (log n) 。

非遞迴作法

樹的遍歷，本質上是在做 DFS ，因此需要 stack 來搭配使用，死記程式碼絕對不是好方法，試想看看我們的腦袋是怎麼做中序遍歷的。

1. 首先一定是先將左子樹走到底，途中經過的所有 root 節點及其右子樹都還需要處理，因此需將 root 節點們放至 stack 中 ，有了 root 節點等於也把右子樹都記錄下來。
2. 當左子樹無路可走時，根據中序遍歷規則，接下來應該處理的是中間 root 節點，因此從 stack 拿出一個剛剛存下的節點 ( n-1 層的左子樹節點就是第 n 層的中間節點)。
3. 處理完 root ，接著將 root 指向其右子樹節點，這時又來到一個新的子樹，因此又再回到步驟 1 。

public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        while (root != nullptr || !st.empty())
        {
            while (root != nullptr)
            {
                st.push (root);
                root = root->left;
            }
            root = st.top();
            st.pop();
            result.push_back(root->val);
            root = root->right;
        }
        return result;
    }

空間複雜度 & 時間複雜度

均為 O(n)

• 可以透過 Leetcode #94, #99, #173, #426 和 #897 來檢驗自己是否學會中序遍歷。

前序遍歷

前序遍歷的遞迴作法相當簡單，我們就不解釋，來探討非遞迴作法。
前序遍歷實際上就是在做 DFS ，DFS 的精神是先遇到的就先走，在 binary tree 上進行前序遍歷，就等同先遇到先走，先遇到 root 節點，接下來往左子樹走下去，左子樹的 root 節點又被視為下一個搜尋起點，繼續走下去，完全就是最正統的 DFS 走法。
比較需要注意的是，從 stack pop 出節點，要先放右節點到 stack 中，再放左節點。

vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode *> st;

        if (root != nullptr)
        {
            st.push (root);
        }
        while (!st.empty())
        {
            root = st.top();
            st.pop();
            result.push_back (root->val);

            if (root->right != nullptr)
            {
                st.push (root->right);
            }
            if (root->left != nullptr)
            {
                st.push (root->left);
            }
        }
        return result;
    }

時間複雜度 & 空間複雜度

O (n)

• 可以透過 Leetcode #144 來檢驗自己是否學會 preorder traversal

後序遍歷

後序遍歷的遞迴方式相當簡單，我們就不探討，來探討非遞迴作法，非遞迴的後序遍歷並不好處理，可以應用 reverse post-order 的思考邏輯來處理。

以 reverse post-order 出來的結果，再執行一次 reverse 後結果就等同於 Post order 。

post order 處理順序 ： left →right →root

reverse post-order 處理順序： root →right →left

可以觀察到， reverse post-order 跟處理 preorder 相當類似，差別在於左右子樹的處理順序而已。 至於 reverse 的動作，我們可以藉助 deque ， deque 是 C++ STL 內的標準資料結構，可以透過 deque.push_front() 達到反向插入新元素的效果，以下展示程式碼。

vector<int> postorderTraversal(TreeNode* root) {
        deque<int> dq;
        stack<TreeNode *> st;

        if (root != nullptr)
        {
            st.push (root);
        }
        while (!st.empty())
        {
            root = st.top();
            st.pop();
            dq.push_front (root->val);
            if (root->left != nullptr)
            {
                st.push (root->left);
            }
            if (root->right != nullptr)
            {
                st.push (root->right);
            }
        }
        return vector<int>(dq.begin(), dq.end());
    }

• 可以透過 Leetcode #145 來檢驗自己是否學會 postorder traversal

時間複雜度 & 空間複雜度

O(N)

Updated on 2022-05-22 18:02:23 星期日